PERSAMAAN KUADRAT
v Pengertian Persamaan Kuadrat
 Bentuk Umum Persamaan Kuadrat
Bentuk Umum Persamaan KuadratDimana a, b, c є R dan a ≠ 0.
Koefisien x2 konstanta
Koefisien x
Bentuk Lain Persamaan Kuadrat :

Dengan demikian persamaan kuadrat adalah persamaan berderajat dua dalam x
v Cara- cara Menyelesaikan Persamaan Kuadrat
a. Memfaktorkan
untuk bentuk ax2 + bx + c = 0), maka kalian harus menentukan dua buah bilangan yang jumlahnya b dan hasil kalinya c
b. Melengkapkan kuadrat sempurna
ialah mengubah suatu bentuk kuadrat menjadi bentuk kuadrat sempurna.
Misalnya x2 – 2x diubah menjadi bentuk kuadrat sempurna x2 – 2x + 1 = (x - 1)
c.  Menggunakan rumus kuadrat
Menggunakan rumus kuadrat
 Menggunakan rumus kuadrat
Menggunakan rumus kuadrat Dengan b2 – 4ac ≥
Jika b2 – 4ac < 0 maka persamaan kuadrat tidak memiliki penyelesaian
Jika b2 Jika b2 – 4ac = 0 maka persamaan kuadrat memiliki tepat satu penyelesaian
Jika b2 – 4ac > 0 maka persamaan kuadrat memiliki dua penyelesaian
v Menyusun Persamaan Kuadrat
|
Ø Memakai faktor :
Ø Memakai rumus jumlah dan hasil kali akar-akar
Diperoleh dari penjumlahan dan perkalian rumus abc
x1 + x2 = -b + √ b2 – 4ac + - b - √ b2 – 4ac
2a 2a
= -2b
2a
= -b
a
x1 x x2 = -b + √ b2 – 4ac x - b - √ b2 – 4ac
2a 2a
= b2 – (b2 – 4 ac)
4a2
= 4ac
4a2
= c
a
|
Sehingga dapat dinyatakan
Contoh
Contoh 1 :
☺ Bagaimana merubah persamaan 2x2 = 3x - 8 ke dalam bentuk umum???
Penyelesaian : 2x2 = 3x – 8
<=> 2x2 - 3x = 3x-3x -8 (kedua ruas dikurangi 3x)
<=> 2x2 – 3x = -8
<=> 2x2 - 3x + 8 = -8 + 8 (kedua ruas ditambah 8)
<=> 2x2 – 3x + 8 = 0
Jadi a = 2, b = - 3 dan c = 8
Contoh 2 :
Cara memfaktorkan
Contoh : x2 – 5 x + 6 = 0
<=> ( x-2 ) ( x-3 ) = 0
<=> x- 2 = 0 atau x - 3 = 0
<=> x = 2 atau x = 3
Sehingga himpunan penyelesaiannya adalah {2, 3}
Contoh 3
Cara Melengkapakan Kuadrat
Contoh : Menentukan himpunan penyelesaian dari persamaan x2 + 2x – 15 = 0 !
Jawab : x2 + 2x – 15 = 0
x2 + 2x = 15
Agar x2 + 2x menjadii bentuk kuadrat sempurna, harus ditambah dengan kuadrat dari setengah koefisien x + (½ x 2)2 = 12 = 1
Dengan menambahkan 1 pada kedua ruas, diperoleh :
x2 + 2x + 1 = 15 + 1
<=> (x + 1)2 = 16
<=> x + 1 = ± √16
<=> x + 1 = ± 4
<=> x + 1 = 4 atau x + 1 = -4
<=> x = 4 - 1 atau x = -4 -1
<=> x = 3 atau x = -5
Jadi, himpunan penyelesaiannya adalah {3, -5}
Contoh 4
a. Menggunakan rumus kuadrat
Menentukan himpunan penyelesaian persamaan x2 + 4x – 12 = 0
a =1 b = 4 c = -12
penyelesaian
x1,2 = - b ± √b2 – 4ac
2a
<=> x1,2 = - 4 ± √42 – 4 x 1x (-12)
2 x 1
<=> x1,2 = - 4 ± √16 + 48
2
<=> x1,2 = - 4 ± √64
2
<=> x1,2 = - 4 ± 8
2
<=> x1,2 = - 4 + 8 atau x1,2 = - 4 - 8
2 2
<=> x1 = 2 atau x2 = -6
jadi himpunan penyelesaiannya adalah {-6, 2}
Contoh 5 : Bagaimana menetukan persamaan kuadrat yang akar-akarnya 2 dan 5???
Cara 1 : x1 = 2 dan x2 = 5
Maka (x-x1) (x-x2) = 0
<=> (x-2) (x-5) = 0
<=> x2 – 7x + 10 = 0
Jadi persamaan kuadratnya x2 – 7x + 10 = 0
Cara 2 : x1 = 2 dan x2 = 5
Maka x2 – (x1+x2)x + x1.x2 = 0
Dengan (x1 + x2) = 2 + 5 = 7
x1. x2 = 2.5 = 10
Jadi persamaan kuadratnya x2 – 7x + 10 = 0
Contoh 6 : penerapan Persamaan Kuadrat
Luas sebidang tanah berbentuk persegi panjang, yaitu 4.320 m2. Jika panjang tanah itu 12m lebih panjang daripada lebarnya, berapakah panjang dan lebar tanah tersebut?
Penyelesaian :
Misalnya panjang tanah x meter dan lebar 4 meter maka
Y = ( x- 12) meter
Luas tanah = x . y
4.320 = x . y
<=> 4.320 = x . (x-12)
<=> x2 – 12x – 4320 = 0
<=> (x- 72) (x + 60) = 0
<=> x - 72 = 0 atau x + 60 = 0
<=> x = 72 atau x = - 60
karena panjang tanah harus positif, nilai yang memenuhi adalah x = 72.
Untuk x = 72 maka y = x – 12 = 72 – 12 = 60
Jadi, panjang tanah adalah 72 meter dan lebar tanah adalah 60 meter.
LATIHAN
☺ Nyatakan persamaan 2 (x2 + 1) = x (x + 3) ke dalam bentuk umum persamaan kuadrat !
☺ Tentukan himpunan penyelesaian persamaan kuadrat 2x2 – 5x – 3 = 0, jika x є R!
☺ Tentukan persamaan kuadrat jika diketahui akar-akarnya adalah 3 dan 0 !
☺ Jumlah dua bilangan cacah adalah 12. jika hasil kali dua bilangan itu 35. Tentukan kedua bilangan cacah yang dimaksud !
Pemyelesaian
1) 2 (x2 + 1) = x (x + 3)
<=> 2x2 + 2 = x2 + 3x
<=> 2x2 – x2 + 2 = x2 – x2 + 3x (kedua ruas dikurangi x2)
<=> x2 + 2 = 3x
<=> x2 – 3x + 2 = 3x – 3x (kedua ruas dikurangi 3x)
<=> x2 – 3x + 2 = 0
Jadi, a = 1, b = -3, dan c = 2
2) Dua bilangan yang jumlahnya -5
Dan hasil kalinya 2 x (-3) = -6 adalah 1 dan -6 sehingga diperoleh
2x2 – 5x – 3 = 0
<=> (2x + 1) (2x – 6) = 0
<=> 2x + 1 = 0 atau 2x – 6 = 0
<=> x = - 1 atau x = 3
2
Jadi HP = {- 1, 3}
2
3) dengan cara memfaktor
x1 = 3 dan x2 = 0
(x - x1) (x – x2) = 0
(x – 3) (x-0) = 0
x (x – 3) = 0
x2 – 3x = 0
Jadi, persamaan kuadrat yang dimaksud adalah x2 – 3x = 0
4) Misalkan kedua bilangan itu x dan y maka x + y = 12
Dan xy = 35. Oleh karena itu, kita peroleh persamaan berikut :
x (12 – x) = 35 (karena y = 12 – x)
<=> 12x – x2 = 35
<=> x2 – 12 = -35
<=> x2 – 12x 36 = -35 +36
<=> (x – 6)2 = 1
<=> x – 6 = ±1
<=> x - 6 = 1 atau x – 6 = -1
<=> x = 1 = 6 atau x = -1 + 6
<=> x = 7 atau x = 5
jika x = 7 maka y = 12 - 7 = 5
jika x = 5 maka y = 12 – 5 = 7
jadi, kedua bilangan yang dimaksud adalah 5 dan 7

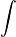








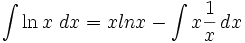





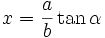

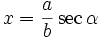









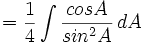
 dengan menggunakan substitusi
dengan menggunakan substitusi






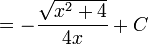





 dan
dan